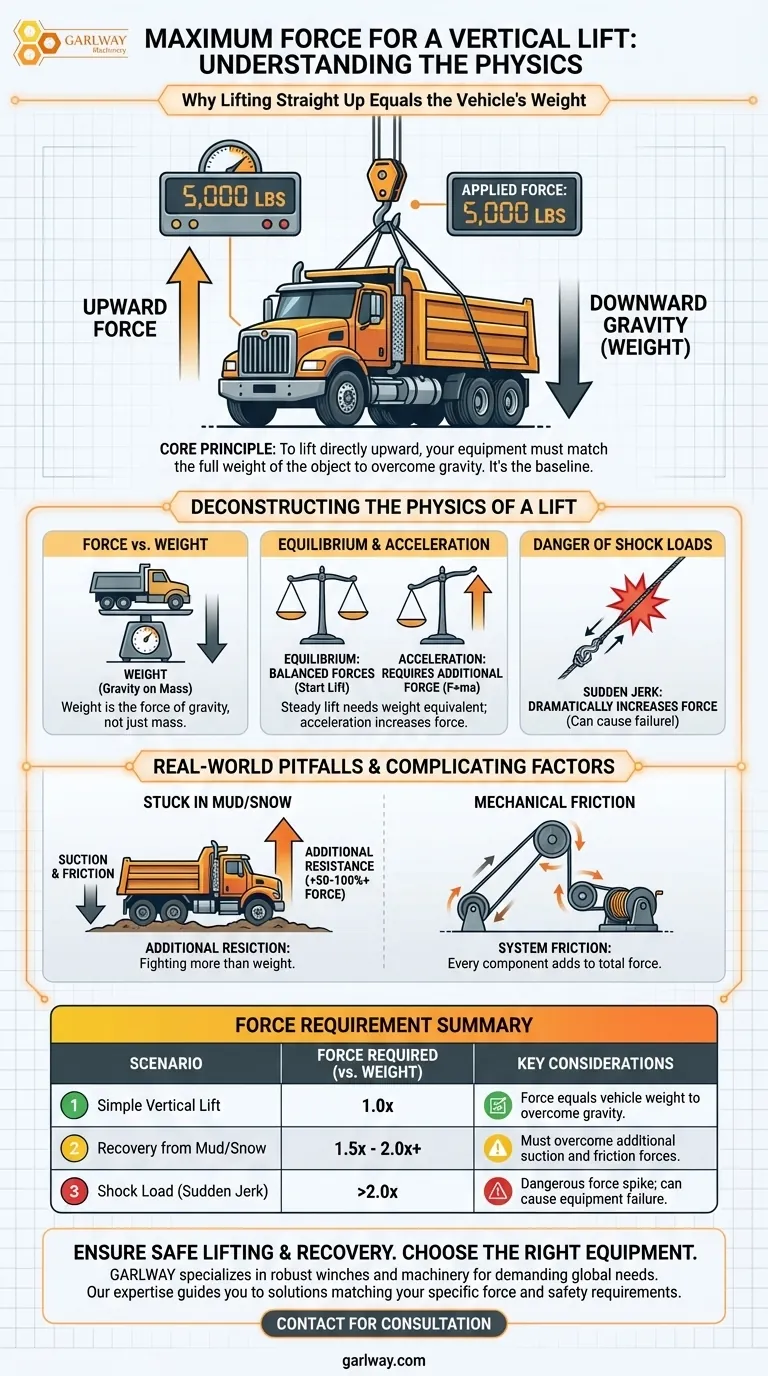
En términos más sencillos, la fuerza máxima requerida para levantar un vehículo verticalmente es igual al peso del propio vehículo. Si un camión pesa 5,000 libras, necesitas aplicar 5,000 libras de fuerza directamente hacia arriba solo para levantarlo del suelo.
Para superar la fuerza de la gravedad en un levantamiento vertical directo, tu equipo debe ser capaz de igualar el peso total del objeto. Este es un principio fundamental de la física que forma la base para cualquier cálculo de izaje o recuperación.

Desglosando la Física de un Levantamiento Vertical
Comprender por qué la fuerza requerida es igual al peso del vehículo es crucial para una operación segura y efectiva. Esto no es solo una regla general; es una aplicación directa de los principios fundamentales de la física.
Fuerza vs. Peso: La Relación Fundamental
El peso de un vehículo es la medida específica de la fuerza de gravedad que actúa sobre su masa. No es lo mismo que la masa en sí.
Cuando levantas un vehículo, estás aplicando una fuerza hacia arriba para contrarrestar la fuerza descendente de la gravedad (su peso).
El Concepto de Equilibrio
Para comenzar el levantamiento, debes aplicar una fuerza que sea al menos igual al peso del vehículo. Esto crea un estado de equilibrio, donde la fuerza hacia arriba y la fuerza hacia abajo (gravedad) están balanceadas.
Para lograr un movimiento ascendente real, la fuerza aplicada debe ser infinitesimalmente mayor que el peso del vehículo. Para todos los cálculos prácticos relacionados con la capacidad del equipo, consideramos que la fuerza máxima requerida es 1.0 veces el peso del vehículo.
El Papel Crítico de la Aceleración
La Segunda Ley de Newton (Fuerza = Masa × Aceleración) nos dice que cualquier aceleración hacia arriba requiere fuerza adicional.
Levantar un vehículo lenta y constantemente requiere una fuerza igual a su peso. Sin embargo, dar tirones a la línea o intentar levantarlo rápidamente aumentará drásticamente la fuerza requerida, creando una peligrosa "carga de choque".
Errores Comunes y Factores Complicantes
Si bien la física de un levantamiento vertical simple es sencilla, los escenarios del mundo real rara vez son perfectos. Varios factores pueden aumentar la fuerza requerida mucho más allá del peso en vacío del vehículo.
El Peligro de las Cargas de Choque
Un tirón repentino o un "arranque en marcha" en una línea de recuperación puede multiplicar la fuerza ejercida sobre el sistema. Esta carga de choque puede exceder fácilmente el límite de carga de trabajo de los cabrestantes, las cuerdas y los puntos de conexión, lo que lleva a fallas catastróficas.
Resistencia por Estar Atascado
Si un vehículo está atascado en barro, arena o nieve, estás luchando contra algo más que su peso. También debes superar las poderosas fuerzas de succión y fricción.
Esta resistencia adicional puede sumar fácilmente entre un 50% y un 100% (o más) a la fuerza requerida para la extracción en comparación con un simple levantamiento.
Fricción Mecánica en tu Sistema
Cada polea, bloque o cambio de dirección en tu configuración de aparejo introduce fricción. Si bien a menudo es menor, esta fricción se suma a la fuerza total que tu cabrestante o mecanismo de elevación debe generar para mover la carga.
Tomando la Decisión Correcta para tu Tarea
Utiliza esta comprensión de la fuerza para seleccionar el equipo y la estrategia adecuados. Tu objetivo principal dicta cómo debes interpretar la regla de "1.0x el peso del vehículo".
- Si tu enfoque principal es un levantamiento vertical simple y controlado: Tu equipo (grúa, cabrestante, etc.) debe tener un límite de carga de trabajo clasificado para al menos el peso total del vehículo.
- Si tu enfoque principal es la recuperación de barro o nieve: Asume que la fuerza requerida será significativamente mayor que el peso del vehículo y utiliza equipo con un factor de seguridad sustancial (por ejemplo, un cabrestante clasificado para 1.5x a 2.0x el peso del vehículo).
- Si tu enfoque principal es la seguridad en cualquier escenario: Opera siempre lenta y suavemente para evitar someter tu equipo a cargas de choque.
Comprender este principio fundamental te permite planificar tus operaciones de manera segura y efectiva.
Tabla Resumen:
| Escenario | Fuerza Requerida (vs. Peso del Vehículo) | Consideraciones Clave |
|---|---|---|
| Levantamiento Vertical Simple | 1.0x | La fuerza es igual al peso del vehículo para superar la gravedad. |
| Recuperación de Barro/Nieve | 1.5x - 2.0x+ | Debe superar fuerzas adicionales de succión y fricción. |
| Carga de Choque (Tirón Repentino) | >2.0x | Pico de fuerza peligroso; puede causar fallas en el equipo. |
Asegura que tus Operaciones de Izaje y Recuperación Sean Seguras y Efectivas
Elegir el equipo adecuado es fundamental. Los cálculos de fuerza en este artículo son fundamentales para seleccionar cabrestantes y otra maquinaria con la capacidad y los márgenes de seguridad apropiados.
GARLWAY se especializa en el suministro de maquinaria de construcción robusta, incluyendo potentes cabrestantes, mezcladoras de concreto y plantas de dosificación, diseñadas para las exigentes necesidades de empresas constructoras y contratistas a nivel mundial.
Deja que nuestra experiencia te guíe hacia la solución correcta. Contacta a nuestro equipo hoy mismo para una consulta sobre equipos que se ajusten a tus requisitos específicos de fuerza y seguridad.
Guía Visual
Productos relacionados
- Torno Eléctrico e Hidráulico para Aplicaciones de Alta Resistencia
- Polipasto Pequeño Portátil para Remolque
- Cabrestante Warn Cabrestante para Embarcaciones
- Polipasto Eléctrico Pequeño 120V y 240V para Aplicaciones Compactas
- Cabrestante eléctrico para barcos de alta resistencia de 12000 lb
La gente también pregunta
- ¿Cuál es la relación entre el diámetro de un tambor de cabrestante y su velocidad de enrollamiento? Descubra la compensación entre velocidad y potencia
- ¿Cuáles son las implicaciones de costos de los diferentes sistemas de cabrestante? Una guía sobre la inversión total y el retorno de la inversión (ROI)
- ¿Qué equipo adicional se recomienda para la instalación de un cabrestante? Construya un sistema completo y confiable
- ¿Qué usos recreativos creativos han encontrado las personas para los cabrestantes? Más allá de la recuperación de vehículos
- ¿Qué es un cabrestante y cuál es su propósito principal? Desbloquee una potente fuerza de tracción para sus proyectos.
- ¿Cuál es la diferencia entre un molinete y un cabrestante de ancla? Una guía para anclar de forma segura
- ¿Cuáles son los errores comunes de cabrestante que se deben evitar? Una guía para la recuperación segura y eficaz de vehículos
- ¿Qué medidas de seguridad se deben tomar con respecto al personal durante la operación de una grúa? Guía esencial para la protección de los trabajadores



















